900 and 660 percent error (%)
Percentage (%) Error Calculator
How to can you Calculate Percent Error - Step-by-Step Solution
The Percent Calculator (Error) uses this formula:
The terms "experimental" and "theoretical" used in the equation above are commonly replaced with similar terms. Some terms also used for experimental are "measured" or "actual," and for theoretical, the terms "accepted" and "calculated" are frequently used.
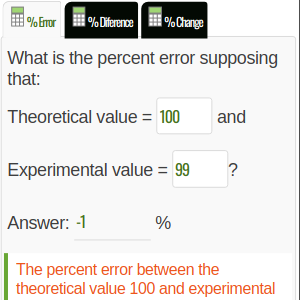
The Percent Error can be a positive or a negative number. If the experimental value is greater than the theoretical value, the result will be positive. On the other hand, if the experimental value is smaller than the theoretical value, the result will be negative. See more about percent error here.
This calculator can answer questions like:
1) What is the percent error supposing 660 as the measured value and 900 as the calculated value?
2) What is the percent error supposing 900 as the measured value and 660 as the calculated value?
3) What is the absolute error between 900 and 660, supposing 900 is the theoretical value? Or maybe: 900 and 660 percent error (%)
See the solutions to these problems below.
1) What is the percent error supposing 660 as the measured value and 900 as the calculated value?
Use the formula above to find the percent error. So, replacing the given values, we have
Percent error = [(660 - 900) / 900] x 100
= (-240 / 900) x 100
= -26.666666666667 % (negative error)
In this case, we have a % of negative error because the experimental is smaller than the theoretical.
2) What is the absolute error between 900 and 660, considering 900 as the theoretical value?
This problem is not about percent or relative error but about absolute error. The solution is very simple:
= 660 - 900 = -240 (negative error)
Percentage (%) Error Calculator
Please link to this page! Just right click on the image below, choose copy link address, then past it in your HTML or in your social media app.